Potenz ist nicht gleich Potenz!
Jüngere haben es wahrscheinlich grad in der Schule, die Älteren müssen wahrscheinlich erst einmal
überlegen. Potenz? - Da war doch mal was! Hallo - nicht diese Potenz, an die ihr gerade denkt
Ist bei manchen Menschen immerhin schon Jahrzehnte her, dass sie damit zu tun hatten
Was sind denn nun Potenzen?
Wir haben also einen Term, der aus der Basis = "a" und dem Exponent "n" besteht. Führt man die beiden
Werte zusammen, erhalten wir den Potenzwert.
Basis a = 5 - Exponent n = 2. Unser Exponentwert ist also 5 hoch 2. In diesem Fall können wir auch
sagen: 5 Quadrat, geschrieben 5².
Es gibt bei den Potenzen bestimmte Gesetzmässigkeiten, die wir unbedingt beachten müssen. Zuerst
aber etwas über unsere Tastatur. In Word oder anderen Textprogrammen gibt es die Funktion
"hochstellen". Damit können wir beliebige Zahlen hochstellen und als Potenzen darstellen. Beim Notepad
oder in anderen Eingabefeldern klappt das aber nicht. Also bedienen wir uns eines besonderen Zeichens:
"^". 5 hoch 5 = 5^5.
Bleiben wir gleich bei 5^5 - dann haben wir 5*5*5*5*5 >>--> die 5 nimmt sich also fünf mal mit sich
selbst mal. Eigentlich eine einfache Multiplikation.
Nun bekommen wir die Aufgabe, zwei Potenzen miteinander zu multiplizieren: 5^5*5^3=?
Da wir eine gleiche Basis, nämlich die 5 haben, ist es einfach. Wir rechnen einfach Basis = x und
Exponent = a, b, ... In unserem Fall also x = 5, a(5) + b(3) = x^a+b oder 5^8.
Was aber tun wir, wenn die Basis bei den Potenzen unterschiedlich, die Exponenten aber gleich sind?
Beispiel: 5^3*7^3 = Lösung: (x*y)^3 = 35^3.
Wir können Potenzen allerdings auch dividieren. Bei gleicher Basis "x" geht das recht einfach; x^a/x^b=
x^a-b - als Zahl sähe das dann so aus: 5^5/5^3= 5^5-3 = 5^2.
Am bekanntesten ist die Verwendung der Potenzen bei Quadrat- und Kubik-Berechnungen. In der
Öffentlichkeit weniger bekannt ist, dass Potenzen benutzt werden um Zins und Zinseszins zu berechnen.
Das ist allerdings dann schon eine andere Baustelle
Prozente
Was bedeuten Prozente? Sie sind Anteile von einem Ganzen! Beispiel: Ich kaufe eine Torte für 7 Personen
und teile diese Torte in 7 gleiche Teile = 100/7*1= 14,29% aufgerundet: Jede der sieben Personen erhält
also einen Anteil von 14,29% der Torte.
Um jetzt für Prozente eine Formel zu entwickeln, müssen wir uns erst einmal auf die für unsere Formel
passenden Buchstaben aussuchen.
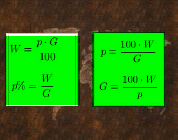
- Wir haben ein Grundwert = G
- dann für den Prozentsatz = p%
- die Prozentzahl nennen wir = p
- der Prozentwert = W
Da es verschiedene Aufgabenstellungen gibt, können wir nun unsere Formeln anhand der
Buchstabenzuweisungen beliebig je nach Bedarf umstellen.
Um bei unserer Torte zu bleiben; nun möchten wir wissen, wie viel Geld wir jedem unserer Gäste mit
seinem Tortenanteil in den Rachen schieben.
Die Torte hat uns 15 Euro gekostet. Nun könnten wir ganz einfach rechnen: 15/7= 2,14 Euro/Stck. Torte.
Da wir das aber auch in Prozenten ausrechnen wollen, rechnen wir
- 100% = 15 Euro
- 1% = 15/100
- 14,29% = (15/100)x14,29
- 14,29% = 2,14 Euro
Unsere Gäste versetzen uns. Doch wir haben Glück. Unser Nachbar möchte auch so eine Torte haben,
aber beim Bäcker sind alle Torten ausverkauft. Wir verkaufen unsere Torte für 17 Euro. Damit haben wir
2 Euro Gewinn gemacht. Wie viel Prozent sind das eigentlich?
Unseren Gewinn bezeichnen wir als "W". Der Grundwert "G" war 15 Euro.
Wir rechnen also: p = (100*w)/g = (100*2)/15 = 13,33% Gewinn!
Josephspfennig und Zinseszins
Im Jahre 1772 hat der englische Ökonom Richard Price seine Gedanken über den Zinseszins in einem
Spiel um den "Josephspfennig" umgesetzt. Er wollte damit aufzeigen, wie sich Kapital, das langfristig
angelegt wird, vervielfacht.
Dabei ging Price davon aus, dass der Vater am Tag der Geburt seines Sohnes Jesus einen Cent angelegt
hatte zu einem jährlichen Zinssatz von 5%. Dieser Cent sollte bis zum heutigen Tag auf der Bank liegen
bleiben und sich dort durch Zins und Zinseszins vermehren.
Gehen wir also von einer Zeit von "nur" 2000 Jahren aus, so rechnet sich das folgendermassen:
Endbetrag = Anfangsbetrag x (1+5/100)^n Jahre.
In unserem Fall:
Endbetrag:? = 1Cent x (1+5/100)^2000
Mit dem Taschenrechner von Windows könnt ihr das leicht selbst berechnen. Dazu den Rechner aufrufen
und auf "wissenschaftlich" stellen.
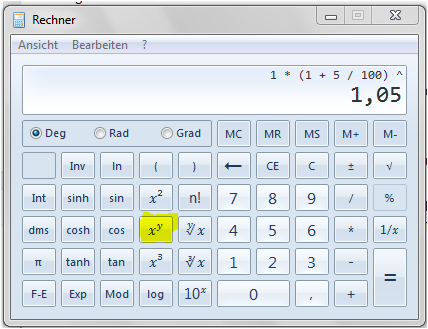
Mit der x^y= x hoch y Funktion den Wert berechnen:
23.911.022.046.136.196.279.738.609.537.102.053.900.288 Euro, das sind fast 24 Sextilliarden Euro!
Sieht man sich diese astronomische Zahl an, dann wird auch klar, dass der Zinseszins sittenwidrig ist.
Denn allein dieser eine Cent wäre im Laufe von 2000 Jahren mehr wert, als das Gesamtvermögen dieser
Welt!
|

